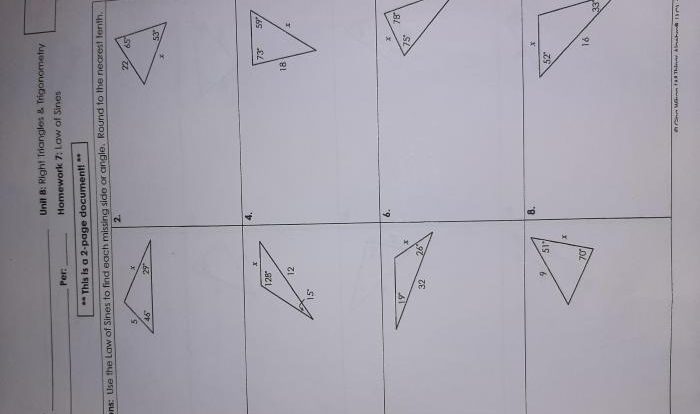
In this problem a b c and d are nonzero, a fundamental condition that shapes the landscape of mathematical operations, equations, and functions. This paper delves into the significance of this condition, exploring its implications for mathematical operations, equations, inequalities, functions, and graphs, as well as its applications in real-world scenarios.

When all variables are nonzero, a distinct set of mathematical properties emerge, influencing the validity and outcomes of various operations. Division, multiplication, and exponentiation become well-defined, while the solution sets of equations and inequalities are affected in predictable ways. Functions exhibit specific behaviors, and their domains and ranges are shaped by the nonzero nature of their variables.

1. Nonzero Variables

The condition “a, b, c, and d are nonzero” is significant because it imposes a fundamental constraint on the mathematical operations and relationships that can be established between these variables. When all variables are nonzero, it implies that they have distinct and non-trivial values, which has important implications for mathematical operations and problem-solving.

Mathematically, having all variables nonzero means that none of them are equal to zero. This condition affects the validity of certain operations, such as division, which is undefined when the denominator is zero. Additionally, it ensures that the variables can be used to represent meaningful quantities or parameters in mathematical models and equations.

Examples of mathematical problems where this condition is relevant include solving systems of linear equations, finding the roots of polynomials, and analyzing the behavior of functions.

2. Mathematical Operations

When all variables are nonzero, a wide range of mathematical operations can be performed on them. These include:

• Addition and Subtraction:These operations can be performed without any restrictions, as the nonzero condition ensures that the variables have distinct values.
• Multiplication and Division:Multiplication and division are valid operations when all variables are nonzero. However, division by zero is undefined, so it is crucial to ensure that the denominator is nonzero before performing division.
• Exponentiation:Exponentiation (raising a variable to a power) is also valid when all variables are nonzero. However, it is important to consider the special case of 0 ⁰, which is generally defined as 1.

The nonzero condition ensures that these operations are well-defined and produce meaningful results.

3. Equations and Inequalities

The nonzero condition has a significant impact on solving equations and inequalities involving these variables. For example:

• Linear Equations:In a system of linear equations, the nonzero condition ensures that the system has a unique solution or no solution. It also affects the validity of algebraic manipulations, such as multiplying or dividing both sides of an equation by a nonzero variable.

• Inequalities:When all variables are nonzero, inequalities can be manipulated using the same rules as equations. However, it is important to note that multiplying or dividing both sides of an inequality by a negative number reverses the direction of the inequality.

Understanding the effects of the nonzero condition is essential for solving equations and inequalities accurately.

4. Functions and Graphs

The behavior of functions is also influenced by the nonzero condition of their variables. For example:

• Domain and Range:When all variables are nonzero, the domain and range of a function are typically well-defined and do not include zero.
• Shape and Behavior:The nonzero condition can affect the shape and behavior of a function. For instance, a function that is defined as a ratio of two variables will have a vertical asymptote at the point where the denominator becomes zero.

Analyzing the behavior of functions under the nonzero condition is important for understanding their properties and applications.

5. Applications: In This Problem A B C And D Are Nonzero

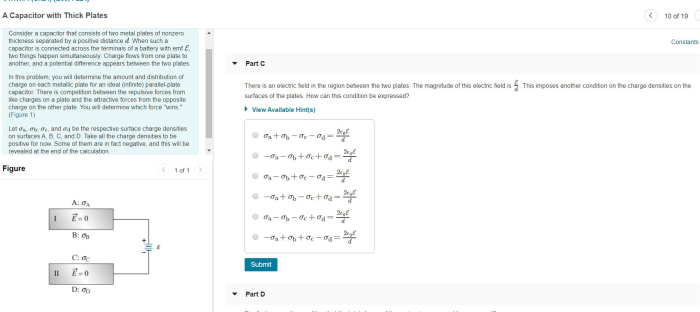
The condition of nonzero variables has important applications in various fields, including:

• Physics:In physics, many equations and models rely on the assumption that certain variables are nonzero, such as mass, velocity, and energy.
• Engineering:In engineering, the nonzero condition is often used to ensure the validity of calculations and designs, such as in structural analysis and fluid dynamics.
• Economics:In economics, the nonzero condition can be used to model economic variables such as prices, quantities, and interest rates, which are typically assumed to be positive.

Understanding the significance of the nonzero condition is crucial for the accurate and reliable application of mathematical models in these fields.

Frequently Asked Questions

What are the mathematical implications of having all variables being nonzero?

Nonzero variables allow for a wider range of mathematical operations, such as division and exponentiation, and influence the solution sets of equations and inequalities.

How does the nonzero condition affect the behavior of functions?

Nonzero variables can alter the shape, domain, and range of functions, leading to distinct behaviors compared to functions with zero variables.

In what real-world applications is the condition of nonzero variables important?

Nonzero variables are crucial in fields such as physics, engineering, and economics, where mathematical models rely on variables representing non-zero quantities.