Embark on a mathematical journey with Unit 7 Right Triangles and Trigonometry Answer Key, an invaluable resource that illuminates the fundamental concepts of trigonometry and its applications. Delve into the realm of right triangles, unravel the mysteries of trigonometric ratios, and master the art of solving real-world problems with this comprehensive guide.
As you navigate through this guide, you will gain a profound understanding of the Pythagorean theorem, trigonometric ratios, the unit circle, and the practical applications of trigonometry in diverse fields such as navigation, engineering, and surveying.
1. Introduction: Unit 7 Right Triangles And Trigonometry Answer Key

Right triangles are triangles with one right angle (90 degrees). Trigonometry is the branch of mathematics that deals with the relationships between the sides and angles of right triangles. Understanding right triangles and trigonometry is essential for many fields, including navigation, engineering, and surveying.
2. Pythagorean Theorem
Definition
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Examples
- If a right triangle has legs of length 3 and 4, then the length of the hypotenuse is sqrt(3^2 + 4^2) = 5.
- If a right triangle has a hypotenuse of length 10 and one leg of length 6, then the length of the other leg is sqrt(10^2 – 6^2) = 8.
Applications
- The Pythagorean theorem can be used to find the distance between two points.
- It can also be used to find the height of a building or the length of a shadow.
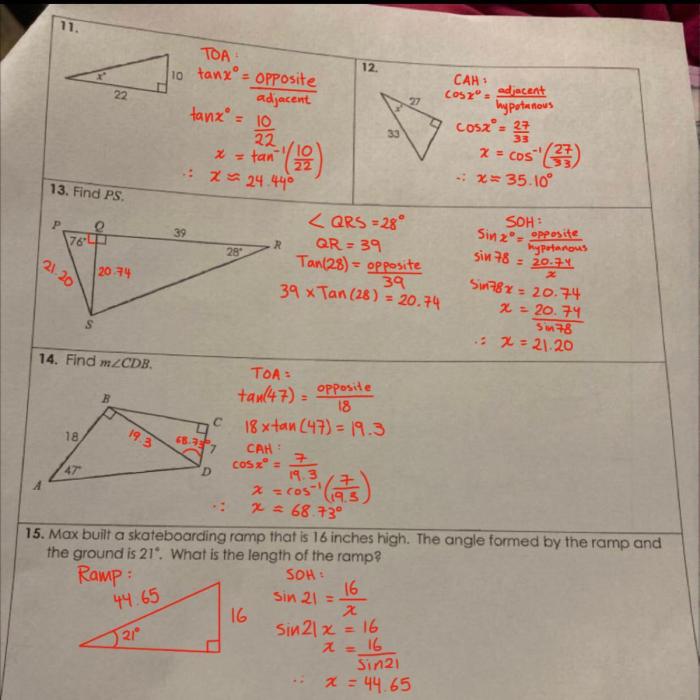
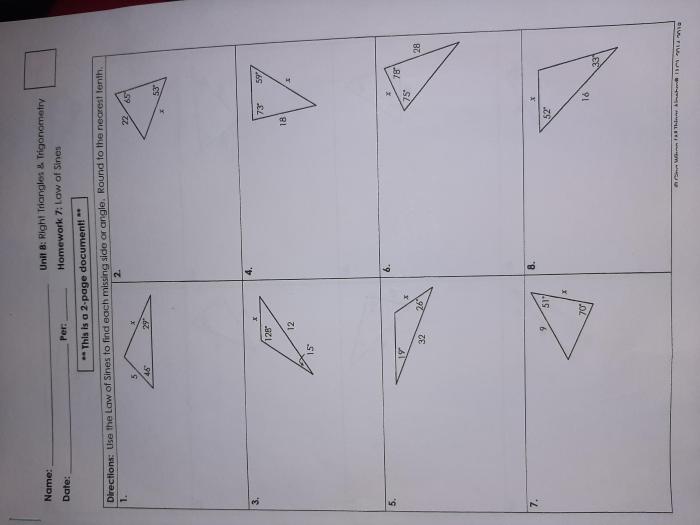
3. Trigonometric Ratios
Definitions
The six trigonometric ratios are sine, cosine, tangent, cosecant, secant, and cotangent. They are defined as follows:
- Sine (sin) = opposite / hypotenuse
- Cosine (cos) = adjacent / hypotenuse
- Tangent (tan) = opposite / adjacent
- Cosecant (csc) = hypotenuse / opposite
- Secant (sec) = hypotenuse / adjacent
- Cotangent (cot) = adjacent / opposite
Calculations
To calculate the trigonometric ratios of an angle, you can use the following formulas:
- sin θ = sin(90° – θ)
- cos θ = cos(90° – θ)
- tan θ = tan(90° – θ)
- csc θ = csc(90° – θ)
- sec θ = sec(90° – θ)
- cot θ = cot(90° – θ)
Examples
- If a right triangle has an angle of 30 degrees and a hypotenuse of length 10, then the length of the opposite side is 10 – sin(30°) = 5.
- If a right triangle has an angle of 60 degrees and an adjacent side of length 6, then the length of the hypotenuse is 6 / cos(60°) = 12.
4. Unit Circle
Definition
The unit circle is a circle with a radius of 1. It is used to find the trigonometric ratios of angles.
Relationship to Trigonometric Ratios, Unit 7 right triangles and trigonometry answer key
The trigonometric ratios of an angle can be found by drawing a right triangle in the unit circle with the angle as one of the angles. The coordinates of the point where the hypotenuse of the triangle intersects the unit circle are the sine and cosine of the angle.
Examples
To find the sine of 30 degrees, draw a right triangle in the unit circle with an angle of 30 degrees. The coordinates of the point where the hypotenuse of the triangle intersects the unit circle are (1/2, sqrt(3)/2). Therefore, the sine of 30 degrees is 1/2.
5. Applications of Trigonometry
Navigation
Trigonometry is used in navigation to find the direction and distance to a destination. For example, a sailor can use trigonometry to find the angle between the direction of the boat and the direction to the destination. The sailor can then use the angle and the distance to the destination to find the course to sail.
Engineering
Trigonometry is used in engineering to design and build structures. For example, an engineer can use trigonometry to find the angle at which a beam must be placed to support a load. The engineer can then use the angle and the load to find the size of the beam.
Surveying
Trigonometry is used in surveying to measure the distance and elevation of objects. For example, a surveyor can use trigonometry to find the distance to a tree. The surveyor can then use the distance and the angle of elevation to find the height of the tree.
Questions and Answers
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
How do I calculate the trigonometric ratios of an angle?
Trigonometric ratios are calculated using the coordinates of a point on the unit circle that corresponds to the angle. The sine is the y-coordinate, the cosine is the x-coordinate, the tangent is the y-coordinate divided by the x-coordinate, the cosecant is the reciprocal of the sine, the secant is the reciprocal of the cosine, and the cotangent is the reciprocal of the tangent.
What are some real-world applications of trigonometry?
Trigonometry is used in navigation to determine the distance and direction to a destination, in engineering to design structures and machines, and in surveying to measure land areas and distances.